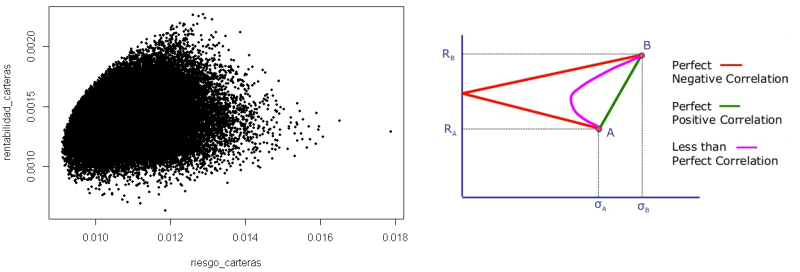
La frontera de Markowitz es el conjunto de carteras eficientes, las cuales ofrecen una mayor rentabilidad esperada según los diferentes niveles de riesgo que se pueden asumir (o el menor riesgo para una rentabilidad esperada).
Se representa gráficamente como una curva, en dónde cualquier cartera que no se encuentre sobre la línea de la frontera no será eficiente, y por lo tanto estará corriendo riesgos innecesarios o recibiendo una rentabilidad inferior a la que podría obtener, con respecto al riesgo que está asumiendo.
La frontera de carteras eficiente representa la relación óptima que encontramos en una cartera de inversión entre volatilidad y rentabilidad, es decir, entre los beneficios que el inversor podrá obtener y los riesgos que deberá afrontar para hacerlo. Y en este problema, la correlación entre activos tiene mucho que decir en la formación de la cartera eficiente.
Cálculo de la frontera de Markowitz con 5 activos y 50.000 simulaciones (programación en R)
# Cargamos los datos
datos <- read.csv("indices.csv", sep=';',stringsAsFactors = FALSE)
activos<- datos[,2:length(datos)] # Extraemos los activos quitando la primera.
# Calculamos la rentabilidad de los activos.
rent_activos<-as.data.frame(matrix(0,nrow=dim(activos)[1],ncol=length(activos),byrow=F))
names(rent_activos)<-names(activos) # Ponemos nombres a las columnas
rownames(rent_activos) <- datos[,1] # Ponemos nombres a las filas.
for (dia in 2:dim(activos)[1]){
for (activo in 1:length(activos)){
rent_activos[dia,activo]<-log(activos[dia,activo]/activos[dia-1,activo])
}
}
rent_activos<-rent_activos[2:dim(activos)[1],1:length(activos)] # Quitamos la primera línea dado que son ceros.
# Calculamos la matriz de correlaciones
matriz_correlaciones<-cor(rent_activos)
# Calculamos la matriz de varianzas / covarianzas.
matriz_var_covarianzas<-cov(rent_activos) # Obtenemos diréctamente la matriz de varianzas covarianzas
# calculamos la rentabilidad, riesgo y eficiencia de N carteras aleatorias.
num_simulaciones <- 50000
matriz_pesos <- as.data.frame(matrix(0,nrow=dim(activos)[1],ncol=length(activos),byrow=F))
names(matriz_pesos)<-names(activos)
rentabilidad_carteras <- c(1:num_simulaciones)
riesgo_carteras <- c(1:num_simulaciones)
eficiencia_carteras <- c(1:num_simulaciones)
progreso <- winProgressBar(title= "Barra de progreso", min = 0, max = num_simulaciones, width=300)
for (cartera in 1:num_simulaciones){
# Sacamos los pesos de la cartera
pesos <- runif(dim(activos)[2], min = 0, max = 100)
pesos[1:dim(activos)[2]]<-(pesos[1:dim(activos)[2]]/sum(pesos)) # Los pesos deben sumar 100%.
matriz_pesos[cartera,1:dim(activos)[2]]<- pesos
# Calculamos la rentabilidad diaria del periodo para cada activo: LN(precio final/ precio inicial)/nº de datos
rent_diaria <-as.data.frame(matrix(0,nrow=1,ncol=length(activos),byrow=F))
names(rent_diaria)<-names(activos) # Ponemos nombres a las columnas
for (activo in 1:length(activos)){ # Una manera más lenta de hacerlo.
rent_diaria[activo]<-log(activos[dim(activos)[1],activo]/activos[1,activo])/dim(rent_activos)[1]
}
# Calculamos la rentabilidad de la cartera según los pesos (suma producto pesos con rentabilidad diaria)
rentabilidad_carteras[cartera]<-sum(pesos*rent_diaria)
# calculamos el riesgo de la cartera (desviación), en función de los pesos.
vector<-matriz_var_covarianzas%*%pesos # Multiplicamos la matriz de cov/var por el vector fila de pesos.
riesgo_carteras[cartera]<-(t(vector)%*%pesos)^0.5 # Riesgo = vector anterior por vector pesos elevado a 0,5
# calculamos la eficiencia de la cartera (pendiente), en función de los pesos.
# (y2 - y1)/(x2-x1) donde Y1 e Y1 son el origen (0,0)
eficiencia_carteras[cartera] <- (rentabilidad_carteras[cartera])/(riesgo_carteras[cartera])
setWinProgressBar(progreso, cartera, title=paste(round(cartera/num_simulaciones*100,0), "%"))
}
close(progreso)
# Graficamos la frontera de Markowitz (riesgo y rentabilidad para cada vector de pesos)
plot(riesgo_carteras,rentabilidad_carteras, cex = .5, pch=19)
# Localizamos la cartera con mayor rentabilidad, menor riesgo y mayor eficiencia.
matriz_pesos$rentabilidad_cartera <-rentabilidad_carteras # Unimos todos los datos en un único DF.
matriz_pesos$riesgo_cartera <-riesgo_carteras
matriz_pesos$eficiencia_cartera <-eficiencia_carteras
max_rentabilidad<-matriz_pesos[matriz_pesos$rentabilidad_cartera==max(matriz_pesos$rentabilidad_cartera),]
min_riesgo<-matriz_pesos[matriz_pesos$riesgo_cartera==min(matriz_pesos$riesgo_cartera),]
max_eficiencia<-matriz_pesos[matriz_pesos$eficiencia_cartera==max(matriz_pesos$eficiencia_cartera),]
max_rentabilidad
min_riesgo
max_eficiencia
- Tiempo de ejecución con 5 activos: 11 minutos
- Tiempo de ejecución con 30 activos: 10 horas con 20 minutos
- Tiempo de ejecución con 100 activos: aproximadamente 2 meses
Hay que tener presente que, a más activos, más simulaciones debemos realizar
Podemos resolver el problema vectorizando todos los cálculos, eliminando los bucles y sacando todos los números aleatorios de una sola vez. Probablemente este enfoque resuelva el problema de tiempo de ejecución. Pongámoslo a prueba.
Cálculo de la frontera de Markowitz con 5 activos y 50.000 simulaciones (programación en R)
# Cargamos los datos
datos <- read.csv("indices.csv", sep=';',stringsAsFactors = FALSE)
activos<- datos[,2:length(datos)] # Extraemos los activos quitando la primera.
# Calculamos la rentabilidad de los activos.
rent_activos<-as.data.frame(matrix(0,nrow=dim(activos)[1],ncol=length(activos),byrow=F))
names(rent_activos)<-names(activos) # Ponemos nombres a las columnas
rownames(rent_activos) <- datos[,1] # Ponemos nombres a las filas.
rent_activos[2:dim(activos)[1],1:length(activos)] <- log(activos[2:dim(activos)[1],1:length(activos)]/activos[2:dim(activos)[1]-1,1:length(activos)])
rent_activos<-rent_activos[2:dim(activos)[1],1:length(activos)] # Quitamos la primera línea dado que son ceros.
# Calculamos la matriz de correlaciones
matriz_correlaciones<-cor(rent_activos)
# Calculamos la matriz de varianzas / covarianzas.
matriz_var_covarianzas<-cov(rent_activos) # Obtenemos diréctamente la matriz de varianzas covarianzas
# Calculamos la rentabilidad diaria del periodo para cada activo: LN(precio final/ precio inicial)/nº de datos
rent_diaria <-as.data.frame(matrix(0,nrow=1,ncol=length(activos),byrow=F))
names(rent_diaria)<-names(activos) # Ponemos nombres a las columnas
rent_diaria<-t(rent_diaria)
activos<-t(activos) # rentabilidad vectorial: traspongo precios para que los activos sean filas y no columnas.
rent_diaria[1:dim(activos)[1]]<-log(activos[1:dim(activos)[1],dim(activos)[2]]/activos[1:dim(activos)[1],1])/dim(rent_activos)[1]
rent_diaria<-t(rent_diaria)
activos<-t(activos)
# Sacamos la matriz de pesos para cada cartera
num_simulaciones <- 50000
pesos <- runif(dim(activos)[2]*num_simulaciones, min = 0, max = 100) # pesos de todas simulaciones de una vez.
pesos <- matrix(pesos, nrow=num_simulaciones, ncol=dim(activos)[2], byrow=TRUE)
pesos[,1:dim(activos)[2]]<-(pesos[,1:dim(activos)[2]]/rowSums(pesos)) # Escalamos los pesos a 1
# Calculamos la rentabilidad de la cartera en función de los pesos
# Para cada conjunto de pesos queremos hacer suma producto de pesos con rentabilidad diaria.
rentabilidad_carteras <- c(1:num_simulaciones) # vector para guardar las rentabilidades de cada cartera.
matriz_intermedia <- matrix(0,nrow=dim(activos)[1],ncol=dim(activos)[2],byrow=F)
matriz_intermedia<-t(as.vector(rent_diaria)*t(pesos)) # Sin as.vector da error al multiplicar dos matrices.
rentabilidad_carteras<-rowSums(matriz_intermedia) # Sumamos las filas para sacar rentabilidad de cada cartera.
# calculamos el riesgo de la cartera (desviación), en función de los pesos.
riesgo_carteras <- c(1:num_simulaciones) # Generamos un vector donde guardaremos el riesgo de cada cartera.
# Multiplicamos la matriz de var/covar por cada fila de la matriz de pesos.
matriz_intermedia <- pesos[1:num_simulaciones,]%*%matriz_var_covarianzas
# Multiplicamos cada fila de la matriz intermedia * cada fila de la matriz pesos y el rdo lo elevamos a 0.5.
# Ojo, la multiplicación es matricial de dos vectores.
matriz_intermedia <- matriz_intermedia * pesos
riesgo_carteras <- rowSums(matriz_intermedia)
riesgo_carteras <- riesgo_carteras^0.5
# calculamos la eficiencia de la cartera (pendiente), en función de los pesos.
eficiencia_carteras <- c(1:num_simulaciones)
eficiencia_carteras[1:num_simulaciones] <- rentabilidad_carteras[1:num_simulaciones]/riesgo_carteras[1:num_simulaciones]
# Graficamos la frontera de Markowitz (riesgo y rentabilidad para cada vector de pesos)
plot(riesgo_carteras,rentabilidad_carteras, cex = .5, pch=19)
# Localizamos la cartera con mayor rentabilidad, menor riesgo y mayor eficiencia.
pesos<-as.data.frame(pesos)
names(pesos)<-names(rent_activos) # Ponemos nombres a las columnas
pesos$rentabilidad_cartera <-rentabilidad_carteras # Unimos todos los datos en un único DF.
pesos$riesgo_cartera <-riesgo_carteras
pesos$eficiencia_cartera <-eficiencia_carteras
max_rentabilidad<-pesos[pesos$rentabilidad_cartera==max(pesos$rentabilidad_cartera),]
min_riesgo<-pesos[pesos$riesgo_cartera==min(pesos$riesgo_cartera),]
max_eficiencia<-pesos[pesos$eficiencia_cartera==max(pesos$eficiencia_cartera),]
- Tiempo de ejecución con 5 activos: 0,44 segundos
- Tiempo de ejecución con 30 activos: 1,67 segundos
- Tiempo de ejecución con 100 activos: aproximadamente 5 segundos
Sin duda hemos resuelto el problema del tiempo de ejecución. Pero si rascamos un poco la superficie, al centrarnos en la mejora de tiempo, hemos perdido el foco del problema y ya no estamos generando la frontera de Markowitz.
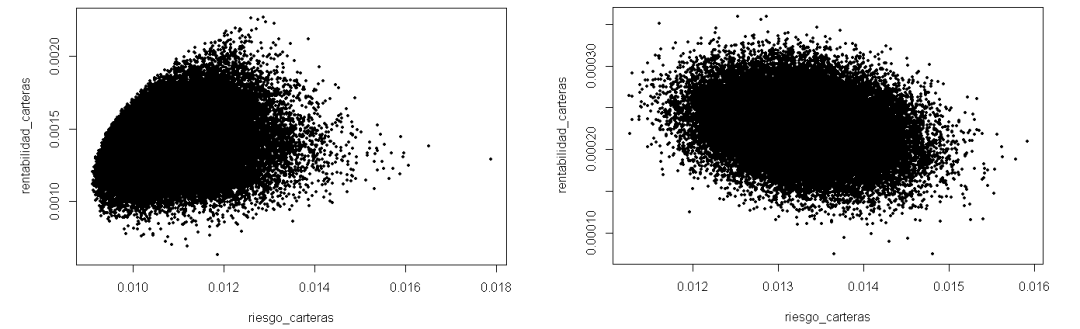
El procedimiento de generación de números aleatorios vectorizado asigna un porcentaje a cada uno de los activos. Posteriormente se transforma a una base 100 por lo que, en todas las simulaciones, todos los activos tienen un porcentaje asignado. De ahí que exista un núcleo central. Prácticamente todos los activos tienen, en todas las simulaciones, el mismo porcentaje invertido. Y este problema se agrava según vamos incrementando el número de activos con los que trabajamos.
¿Qué os parece si tratamos de resolver un reto divertido y calculamos la frontera de Markowitz para 70.000 activos?
Se me ocurren 6 maneras de afrontar este reto:
- Generando carteras aleatorias (enfoque clásico actualizado)
- Aplicando una función cuadrática que aproxima la frontera
- Usando algoritmos genéticos
- Usando algoritmos enjambre
- Aplicando grafos
- Utilizando computación cuántica para la generación de aleatorios
Vamos a tratar de resolver el problema de la cartera óptima empleando las aproximaciones primera y tercera (carteras aleatorias y algoritmos genéticos).
Generando carteras aleatorias (enfoque clásico actualizado en python)
Para resolver el problema se ha utilizado el siguiente ordenador
Alienware Aurora R11, I9-10900KF de 3.70GHz con 10 procesadores y 64 GB de RAM
Antes de empezar, debemos hacernos varias preguntas que tendremos que resolver:
- Los activos no tienen los mismos días cotizados, ¿cómo los homogeneizamos?
- Hay días en los que la mayoría de los activos no tienen cotización ¿qué hacemos?
- ¿Con cuántos activos nos quedamos y por qué?
- ¿Cuántas simulaciones vamos a realizar? trabajamos con muchos activos…
- ¿Cómo generamos los números aleatorios y cuantos generamos? 70.000 activos * 50.000 simulaciones son 3.500 millones de números (más de 10 GB pickle) y 50.000 simulaciones no son suficientes para la cantidad de activos con la que estamos trabajando... tenemos un problema y serio
- ¿Cuántos activos seleccionamos en cada simulación para darles peso?, ¿Cómo los seleccionamos?
- ¿Cómo asignamos peso a los activos seleccionados?
Son preguntas muy importantes, que deberemos ir resolviendo.
Resolviendo el problema de la homogeneización
def homogeizar(datos):
lista_isin = datos.iloc[:,2].unique()
fechas_posibles = datos.date.unique()
fechas_posibles.sort()
fechas_posibles = pd.date_range(fechas_posibles[0], fechas_posibles[-1], freq=BDay())
datos_ordenados = pd.DataFrame(columns=[""], index = fechas_posibles)
for isin in lista_isin:
print(isin)
isin_extraido = extraccion_datos(isin, datos)
# La gran mayoría tiene más de 200 días, pero hay varios con menos de 100 datos
# Debemos filtrar los activos para poder trabajar
if (isin_extraido.shape[0] > fechas_posibles.shape[0]*0.7):
datos_ordenados = pd.concat([datos_ordenados, isin_extraido], axis=1) # alternativa datos_ordenados = datos_ordenados.join(isin_extraido)
datos_ordenados = datos_ordenados.drop(columns='')
# Encontramos las filas donde un % elevado son Nan y las eliminamos
dias_eliminar = ~(datos_ordenados.isna().sum(axis=1) > datos_ordenados.shape[1]*0.9)
datos_ordenados = datos_ordenados.loc[dias_eliminar,:]
# Completamos los Nan con los datos del día anterior
datos_ordenados = datos_ordenados.fillna(method='ffill')
# Aquellos valores que no tienen un primer día cotizado, el método anterior no sirve
datos_ordenados = datos_ordenados.fillna(method='bfill')
datos_ordenados.to_pickle("datos_ordenados.pkl")
return datos_ordenados
Resolviendo el problema de la generación de pesos
num_activos = datos_ordenados.shape[1]
simulaciones = 50000
# Este es el sistema más rápido para generar números aleatorios en python
aleatorios = np.random.randint(low=1, high=100, size=num_activos * simulaciones)
aleatorios = aleatorios.reshape((simulaciones, num_activos))
# Localizamos en cada fila aquellos números que superan un umbral
umbral = 98
aleatorios[aleatorios < umbral] = 0
aleatorios[aleatorios > = umbral] = 1
print(aleatorios.sum(axis=1)) # Sacando así los números aleatorios, cada fila tiene más de 1000 activos seleccionados (este sistema no nos vale)
def generador_pesos(datos_ordenados, simulaciones = 10000):
num_activos = datos_ordenados.shape[1]
aleatorios = np.random.random((simulaciones,num_activos))
umbral = 0.9998
aleatorios[aleatorios < umbral] = 0
# Buscamos y eliminamos las simulaciones que no tienen ningún activo seleccionado
seleccion = ~(aleatorios.sum(axis=1) == 0)
aleatorios = aleatorios[seleccion,:]
# Asignamos los pesos a cada cartera
# Para poder usar los aleatorios, dado que todos los activos seleccionados superan un umbral, debo restar el umbral
# Si reescalase el peso, ningún activo de una cartera de 3 elementos superaría el 50% - 60% de peso. No puedo asignar los pesos reescalando.
aleatorios[aleatorios!=0] = (aleatorios[aleatorios!=0] - umbral) * 10000
for sim in range(aleatorios.shape[0]):
vector_pesos = aleatorios[sim,:]
posiciones = set(np.where(vector_pesos!=0)[0])
# Obtenemos el órden en el que vamos a asignar los pesos
posiciones_aleatorias = random.sample(posiciones, len(posiciones))
peso = 0
for pos in posiciones_aleatorias:
if peso < 1:
peso += aleatorios[sim, pos]
if peso > 1:
exceso = peso - 1
aleatorios[sim, pos] = aleatorios[sim, pos] - exceso
peso = 1
elif peso == 1:
aleatorios[sim, pos] = 0
# En las carteras con 1 o 2 activos, no van a sumar siempre un 100% invertido.
# De cada 10.000 simulaciones, con un umbral de 0.9999 ocurre 600 - 700 veces.
# Con un unbral de 0.9998 de 1 a 5 veces.
# Lo damos por bueno.
return aleatorios
Generando la frontera de Markowitz
def frontera_markowitz(num_simulaciones=100000):
# Cargamos los datos
try:
datos_ordenados = pd.read_pickle("datos_ordenados.pkl")
except:
datos = cargar_ficheros()
comprobacion = comprobar_homogeneizacion(datos)
if comprobacion == False:
datos_ordenados = homogeizar(datos)
# Inicializamos el valor de la cartera más eficiente y preparamos el gráfico de la frontera
eficiencia_inicial = -100
plt.figure(figsize=(20,15))
# Calculamos la rentabilidad de los activos
rent_activos = np.log(datos_ordenados).diff()
rent_activos = rent_activos.iloc[1:,:]
# Calculamos la matriz de correlaciones
try:
matriz_correlaciones = pd.read_pickle("matriz_correlaciones.pkl")
except:
matriz_correlaciones = rent_activos.corr()
matriz_correlaciones.to_pickle("matriz_correlaciones.pkl") # EL pickle ocupa 25,4 GB
# Calculamos la matriz de varianzas / covarianzas
matriz_covarianzas = rent_activos.cov()
matriz_covarianzas = matriz_covarianzas.to_numpy(dtype='float')
# Calculamos la rentabilidad diaria del periodo para cada activo: LN(precio final/ precio inicial)/nº de datos
precio_inicial = datos_ordenados.iloc[0,:]
precio_final = datos_ordenados.iloc[-1,:]
rentabilidad_diaria = np.log(precio_final / precio_inicial) / datos_ordenados.shape[0]
num_bloques = int(np.ceil(num_simulaciones/10000))
for bloque in range(num_bloques):
# Sacamos la matriz de pesos para cada cartera
matriz_pesos = generador_pesos(datos_ordenados, simulaciones = 10000)
# Calculamos la rentabilidad de la cartera en función de los pesos
auxiliar = rentabilidad_diaria.values * matriz_pesos
rentabilidad_carteras = auxiliar.sum(axis=1)
# Calculamos el riesgo de la cartera (desviación), en función de los pesos
auxiliar = np.dot(matriz_pesos, matriz_covarianzas) # Reutilizo la matriz auxiliar con otro propósito para no sobrecargar la RAM
riesgo_carteras = pow((auxiliar * matriz_pesos).sum(axis=1), 0.5)
# Hay que quitar outlayers: quantiles max de riesgo y quantiles minimos de rentabilidad
filtro_riesgo = riesgo_carteras < np.percentile(riesgo_carteras, 99)
riesgo_carteras = riesgo_carteras[filtro_riesgo]
rentabilidad_carteras = rentabilidad_carteras[filtro_riesgo]
filtro_rentabilidad = rentabilidad_carteras > np.percentile(rentabilidad_carteras, 1)
riesgo_carteras = riesgo_carteras[filtro_rentabilidad]
rentabilidad_carteras = rentabilidad_carteras[filtro_rentabilidad]
# Calculamos la eficiencia de la cartera (pendiente), en función de los pesos
# Existen posiciones que van a dar error, 0/0. Las localizo y hago que 0/1 = 0
posiciones_0entre0 = (rentabilidad_carteras==0) * (riesgo_carteras==0)
riesgo_carteras[posiciones_0entre0] = 0.0000001
eficiencia_carteras = rentabilidad_carteras / riesgo_carteras
# Localizamos la cartera con mayor eficiencia
max_eficiencia = max(eficiencia_carteras)
if max_eficiencia > eficiencia_inicial:
posicion_cartera_eficiente = np.where(eficiencia_carteras == max_eficiencia)[0]
cartera_eficiente = matriz_pesos[posicion_cartera_eficiente,:]
posicion_activos_eficientes = np.where(cartera_eficiente!=0)
peso_activos_eficientes = cartera_eficiente[posicion_activos_eficientes]
isin_activos_eficientes = rent_activos.columns.values[posicion_activos_eficientes[1]]
eficiencia_inicial = max_eficiencia
# Graficamos la frontera de Markowitz (riesgo y rentabilidad para cada vector de pesos)
print(f'Iteracion {bloque+1} de {num_bloques}')
plt.plot(riesgo_carteras,rentabilidad_carteras, 'o', color="b")
# Dejamos bonito el gráfico y ajustamos la escala, para ver bien la frontera.
plt.xlabel("Riesgo")
plt.ylabel("Rentabilidad")
scale_factor = 3
xmin, xmax = plt.xlim()
ymin, ymax = plt.ylim()
plt.xlim(xmin * scale_factor, xmax * scale_factor)
plt.ylim(ymin * scale_factor/2, ymax * scale_factor/2)
plt.savefig('frontera_markowitz.png')
return isin_activos_eficientes, peso_activos_eficientes, max_eficiencia
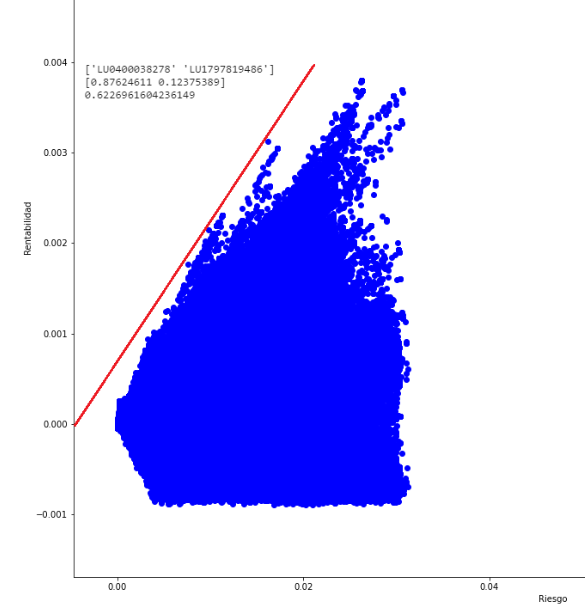
Hemos conseguido generar la frontera de Markowitz, pero para ello hemos necesitado un ordenador muy potente y casi 24 horas para generar 5 millones de carteras aleatorias, teniendo mucho cuidado en los procesos de selección de activos y asignación de pesos.
De hecho, el cálculo de la matriz de covarianzas requiere de 25 GB de memoria RAM, por lo que no es un proceso que esté al alcance de todo el mundo. Ni tampoco parece la solución óptima.
¿Qué alternativas tenemos entonces?
Generando la cartera eficiente a través de algoritmos genéticos (python)
Recapitulando: queremos obtener la cartera óptima de un conjunto de 70.000 activos.
Vamos a intentar resolver el problema usando algoritmos genéticos. Para lo que tendremos que resolver distintos problemas:
Los inversores (cromosomas) deben poder generar carteras con un número variable de activos. Estableceremos el mínimo en 1 activo y 20 en el máximo. El número de activos debe poder modificarse entre generaciones, sin caer en extremos (que siempre salgan carteras de 1 activo o de 20). Debemos pensar un sistema coherente, para resolver este punto.
El método de selección de padres no parece, a priori, problemático, pero el cruce y la mutación sí. ¿Cómo va a heredar el hijo la información genética de los padres? Aquí tenemos un triple problema a resolver:
- ¿Cuál es el número de activos que hereda un hijo de dos padres? Si un padre tiene 5 activos y el otro 7 (distintos entre sí), ¿cuántos activos tendrá el hijo? Debemos pensar en el punto primero. El hijo no puede tener un número de activos creciente en cada generación. El sistema tiene que ser dinámico, creciente y decreciente, respetando los límites de 1 y 20.
- ¿Qué porcentaje de inversión hereda cada activo para que sume 100%? Debemos permitir la construcción de carteras donde unos pocos activos (1 o 2) se lleven un porcentaje muy elevado del capital disponible, para explorar todas las soluciones. Reescalar los pesos no es una solución aceptable.
- La evolución, en este problema no puede limitarse a selección y cruzamiento o caeremos rápidamente en un mínimo local. Debemos encontrar un sistema que equilibre la selección con la exploración, si queremos encontrar la cartera óptima.
Manos a la obra:
Generamos la población inicial
def frontera_markowitz(num_simulaciones=100000):
# Cargamos los datos
try:
datos_ordenados = pd.read_pickle("datos_ordenados.pkl")
except:
datos = cargar_ficheros()
comprobacion = comprobar_homogeneizacion(datos)
if comprobacion == False:
datos_ordenados = homogeizar(datos)
# Inicializamos el valor de la cartera más eficiente y preparamos el gráfico de la frontera
eficiencia_inicial = -100
plt.figure(figsize=(20,15))
# Calculamos la rentabilidad de los activos
rent_activos = np.log(datos_ordenados).diff()
rent_activos = rent_activos.iloc[1:,:]
# Calculamos la matriz de correlaciones
try:
matriz_correlaciones = pd.read_pickle("matriz_correlaciones.pkl")
except:
matriz_correlaciones = rent_activos.corr()
matriz_correlaciones.to_pickle("matriz_correlaciones.pkl") # EL pickle ocupa 25,4 GB
# Calculamos la matriz de varianzas / covarianzas
matriz_covarianzas = rent_activos.cov()
matriz_covarianzas = matriz_covarianzas.to_numpy(dtype='float')
# Calculamos la rentabilidad diaria del periodo para cada activo: LN(precio final/ precio inicial)/nº de datos
precio_inicial = datos_ordenados.iloc[0,:]
precio_final = datos_ordenados.iloc[-1,:]
rentabilidad_diaria = np.log(precio_final / precio_inicial) / datos_ordenados.shape[0]
num_bloques = int(np.ceil(num_simulaciones/10000))
for bloque in range(num_bloques):
# Sacamos la matriz de pesos para cada cartera
matriz_pesos = generador_pesos(datos_ordenados, simulaciones = 10000)
# Calculamos la rentabilidad de la cartera en función de los pesos
auxiliar = rentabilidad_diaria.values * matriz_pesos
rentabilidad_carteras = auxiliar.sum(axis=1)
# Calculamos el riesgo de la cartera (desviación), en función de los pesos
auxiliar = np.dot(matriz_pesos, matriz_covarianzas) # Reutilizo la matriz auxiliar con otro propósito para no sobrecargar la RAM
riesgo_carteras = pow((auxiliar * matriz_pesos).sum(axis=1), 0.5)
# Hay que quitar outlayers: quantiles max de riesgo y quantiles minimos de rentabilidad
filtro_riesgo = riesgo_carteras < np.percentile(riesgo_carteras, 99)
riesgo_carteras = riesgo_carteras[filtro_riesgo]
rentabilidad_carteras = rentabilidad_carteras[filtro_riesgo]
filtro_rentabilidad = rentabilidad_carteras > np.percentile(rentabilidad_carteras, 1)
riesgo_carteras = riesgo_carteras[filtro_rentabilidad]
rentabilidad_carteras = rentabilidad_carteras[filtro_rentabilidad]
# Calculamos la eficiencia de la cartera (pendiente), en función de los pesos
# Existen posiciones que van a dar error, 0/0. Las localizo y hago que 0/1 = 0
posiciones_0entre0 = (rentabilidad_carteras==0) * (riesgo_carteras==0)
riesgo_carteras[posiciones_0entre0] = 0.0000001
eficiencia_carteras = rentabilidad_carteras / riesgo_carteras
# Localizamos la cartera con mayor eficiencia
max_eficiencia = max(eficiencia_carteras)
if max_eficiencia > eficiencia_inicial:
posicion_cartera_eficiente = np.where(eficiencia_carteras == max_eficiencia)[0]
cartera_eficiente = matriz_pesos[posicion_cartera_eficiente,:]
posicion_activos_eficientes = np.where(cartera_eficiente!=0)
peso_activos_eficientes = cartera_eficiente[posicion_activos_eficientes]
isin_activos_eficientes = rent_activos.columns.values[posicion_activos_eficientes[1]]
eficiencia_inicial = max_eficiencia
# Graficamos la frontera de Markowitz (riesgo y rentabilidad para cada vector de pesos)
print(f'Iteracion {bloque+1} de {num_bloques}')
plt.plot(riesgo_carteras,rentabilidad_carteras, 'o', color="b")
# Dejamos bonito el gráfico y ajustamos la escala, para ver bien la frontera.
plt.xlabel("Riesgo")
plt.ylabel("Rentabilidad")
scale_factor = 3
xmin, xmax = plt.xlim()
ymin, ymax = plt.ylim()
plt.xlim(xmin * scale_factor, xmax * scale_factor)
plt.ylim(ymin * scale_factor/2, ymax * scale_factor/2)
plt.savefig('frontera_markowitz.png')
return isin_activos_eficientes, peso_activos_eficientes, max_eficiencia
Calculamos la función de fitness
def calcular_fitness(datos_ordenados, posiciones):
# La función objetivo del AG es maximizar la eficiencia de la cartera (su relación rentabilidad / riesgo)
datos = datos_ordenados.iloc[:,list(posiciones)]
# Calculamos la rentabilidad de los activos
rent_activos = np.log(datos).diff()
rent_activos = rent_activos.iloc[1:,:]
# Calculamos la matriz de correlaciones
matriz_correlaciones = rent_activos.corr()
# Calculamos la matriz de varianzas / covarianzas
matriz_covarianzas = rent_activos.cov()
matriz_covarianzas = matriz_covarianzas.to_numpy(dtype='float')
# Calculamos la rentabilidad diaria del periodo para cada activo: LN(precio final/ precio inicial)/nº de datos
precio_inicial = datos.iloc[0,:]
precio_final = datos.iloc[-1,:]
rentabilidad_diaria = np.log(precio_final / precio_inicial) / datos.shape[0]
# Sacamos la matriz de pesos para cada cartera
matriz_pesos = asignar_pesos(posiciones)
# Calculamos la rentabilidad de la cartera en función de los pesos
auxiliar = rentabilidad_diaria.values * matriz_pesos
rentabilidad_cartera = auxiliar.sum(axis=1)
# Calculamos el riesgo de la cartera (desviación), en función de los pesos
auxiliar = np.dot(matriz_pesos, matriz_covarianzas) # Reutilizo la matriz auxiliar con otro propósito para no sobrecargar la RAM
riesgo_cartera = pow((auxiliar * matriz_pesos).sum(axis=1), 0.5)
# Calculamos la eficiencia de la cartera (pendiente), en función de los pesos
# Existen posiciones que van a dar error, 0/0. Las localizo y hago que 0/1 = 0
posiciones_0entre0 = (rentabilidad_cartera==0) * (riesgo_cartera==0)
riesgo_cartera[posiciones_0entre0] = 0.0000001
eficiencia_cartera = rentabilidad_cartera / riesgo_cartera
# Localizo la cartera de mayor eficiencia y sus pesos correspondientes
posicion_cartera_eficiente = np.where(eficiencia_cartera == eficiencia_cartera.max())
eficiencia_cartera = eficiencia_cartera.max()
pesos_cartera_eficiente = matriz_pesos[posicion_cartera_eficiente,:]
return eficiencia_cartera, pesos_cartera_eficiente
Realizamos la selección de padres
def seleccion_padres(lista_fitness):
# Normalizamos con el método Min - Max para que los valores de la eficiencia estén entre 0 y 1
fitness_normalizado = np.asarray(lista_fitness)
fitness_normalizado = (fitness_normalizado - fitness_normalizado.min()) / (fitness_normalizado.max() - fitness_normalizado.min())
# El órden en el que se van a evaluar los cromosomas para ser seleccionados debe ser aleatorio
orden_aleatorio = random.sample(range(len(fitness_normalizado)), len(fitness_normalizado))
padres_seleccionados = list()
for candidato in orden_aleatorio:
# Sacamos un número entre 0 y 1 y lo comparamos con el valor de fitness_normalizado del candidato
# El valor de fitness actúa como un umbral
# Si el aleatorio es menor al fitness, el candidato se convierte en uno de los dos padres
# De esta manera todos los candidatos tienen posibilidades de ser padre
# los que tienen mayor valor de fitness, son los que tienen más probabilidad de tener descendencia.
aleatorio = np.random.random()
if fitness_normalizado[candidato] > aleatorio:
padres_seleccionados.append(candidato)
if len(padres_seleccionados) == 2:
break
return padres_seleccionados
Cruzamiento y mutación
def cruzamiento(datos_ordenados, lista_posiciones, lista_pesos_carteras_fitness, padres_seleccionados, umbral = 0.4, num_act_max = 20):
'''
Las técnicas habituales de cruzamiento en algoritmos genéticos (N-puntos, segmentación, uniforme y aleatorio) no parecen apropiadas para resolver este problema
Queremos generar un sitema que cruce la información genética de los padres, permitiendo que el tamaño (número de activos) del hijo difiera del de los padres (sin tener que ser forzosamente mayor)
EL sistema de cruzamiento debe centrarse en la selección de activos y no en los pesos. Dado que los pesos serán calculados durante la función de fitness
Hemos usado en las funciones previas dos de los elementos más importantes para resolver el problema: pesos y eficiencia (relación rentabilidad riesgo)
Para hacer el cruzamiento, debemos usar el último elemento importante que queda: la correlación (medida normalizada de la covarianza)
Pasos a dar
1) Nos quedamos con los activos de los padres que tengan peso (el resto los descartamos)
2) Comprobamos que no existen activos repetidos
3) Calculamos la matriz de correlaciones de los activos
4) De aquel conjunto de activos que sean muy correlados, nos quedaremos únicamente con el activo más eficiente (rentabilidad / riesgo)
5) Aplicamos la función de mutación para resolver el problema de la exploración (ver documentación de la función)
6) Comprobamos que el número de activos no supera el máximo permitido y devolveremos las posiciones de los activos que hereda el hijo
'''
# Nos quedamos con los activos de los padres que tengan peso (el resto los descartamos)
posiciones_activos_con_peso_papa = np.where(lista_pesos_carteras_fitness[padres_seleccionados[0]] != 0)
posiciones_activos_con_peso_mama = np.where(lista_pesos_carteras_fitness[padres_seleccionados[1]] != 0)
activos_con_peso_papa = lista_posiciones[padres_seleccionados[0]][posiciones_activos_con_peso_papa[2]]
activos_con_peso_mama = lista_posiciones[padres_seleccionados[1]][posiciones_activos_con_peso_mama[2]]
# Comprobamos que no existen activos repetidos
activos_con_peso = np.unique(np.append(activos_con_peso_papa, activos_con_peso_mama))
activos_con_peso
# Calculamos la rentabilidad y riesgo para el periodo de los activos
datos = datos_ordenados.iloc[:,activos_con_peso]
precio_inicial = datos.iloc[0,:]
precio_final = datos.iloc[-1,:]
rent_global_activos = np.log(precio_final / precio_inicial)
riesgo_global_activos = np.std(datos, axis=0)
eficiencia_global_activos = rent_global_activos / riesgo_global_activos
# Calculamos la matriz de correlaciones de los activos
rent_activos = np.log(datos).diff()
rent_activos = rent_activos.iloc[1:,:]
matriz_correlaciones = rent_activos.corr()
# Calculamos un umbral, a partir del cual descartaremos activos por ser demasiado similares
# Cuanto más descorrelados estén los activos, más eficiente será la cartera, por lo que premiamos la descorrelación
# De aquel conjunto de activos que sean muy correlados, nos quedaremos únicamente con el activo más eficiente (rentabilidad / riesgo)
relaciones_a_analizar = matriz_correlaciones[np.logical_and(matriz_correlaciones > umbral, matriz_correlaciones != 1)]
relaciones_a_analizar = np.where(matriz_correlaciones == relaciones_a_analizar)
if len(relaciones_a_analizar[0]) > 0:
# Recorro todas las relaciones a analizar y fabrico una lista de los activos a quitar (soy consciente de que las relaciones están duplicadas)
activos_a_eliminar = list()
for pos in range(len(relaciones_a_analizar[0])):
if eficiencia_global_activos[relaciones_a_analizar[0][pos]] > eficiencia_global_activos[relaciones_a_analizar[1][pos]]:
activos_a_eliminar.append(relaciones_a_analizar[1][pos])
else:
activos_a_eliminar.append(relaciones_a_analizar[0][pos])
activos_a_eliminar = list(set(activos_a_eliminar))
activos_con_peso = np.delete(activos_con_peso, activos_a_eliminar)
# Aplicamos la función de mutación para resolver el problema de la exploración
nuevos_activos = mutacion(datos_ordenados, activos_con_peso, num_act_max = 20)
activos_heredados = np.unique(np.append(activos_con_peso, nuevos_activos))
# Comprobamos que el número de activos no supera el máximo permitido y devolveremos las posiciones de los activos que hereda el hijo
# Tal y como está programado no debería de ocurrir, pero por si acaso. Si ocurriese mucho, habría que modificar el umbral
if len(activos_heredados) > num_act_max:
seleccion_aleatoria = random.sample(range(len(activos_heredados)), len(activos_heredados))[0:20]
activos_heredados = activos_heredados[seleccion_aleatoria]
return activos_heredados
def mutacion(datos_ordenados, activos_con_peso, num_act_max = 20):
'''
La evolución, en este problema no puede limitarse a selección y cruzamiento o caeremos rápidamente en un mínimo local
Debemos encontrar un sistema que equilibre la selección con la exploración, si queremos encontrar la cartera óptima
Una solución sería que un % del genoma se herede y el resto se dedique a la exploración
Un 20% sobre la cantidad máxima de activos parece un umbral máximo aceptable para combinar las tareas de evolución y exploración
Sacaremos un número aleatorio entre 1 y 4, que serán los nuevos activos para explorar el conjunto de soluciones posibles
'''
num_nuevos_activos = np.random.randint(low=1, high=4, size=1)
nuevos_activos = np.random.randint(low=0, high=datos_ordenados.shape[1]-1, size=num_nuevos_activos)
return nuevos_activos
Reemplazo generacional
def reemplazo_generacional(datos_ordenados, lista_posiciones, lista_fitness, lista_pesos_carteras_fitness, activos_cartera_mejor_individuo):
'''
La estrategia de reemplazo generacional que vamos a utilizar es reemplazo total.
La generación de hijos reemplaza a sus padres, a excepción del mejor de la generación anterior.
'''
# Rellenamos la matriz de descendencia, la cual será una lista con la composición de activos de cada individuo
matriz_descendencia = list()
matriz_descendencia.append(activos_cartera_mejor_individuo)
for hijo in range(len(lista_posiciones)-1):
# Seleccionamos los padres
padres_seleccionados = seleccion_padres(lista_fitness)
# Aplicamos el cruzamiento y la mutación
activos_heredados = cruzamiento(datos_ordenados, lista_posiciones, lista_pesos_carteras_fitness, padres_seleccionados, umbral = 0.4, num_act_max = 20)
# Añadimo el nuevo hijo a la matriz de descendencia
matriz_descendencia.append(activos_heredados)
# Para que el algoritmo pueda ejecutarse de manera circular, la matriz de descendencia se ha de llamar lista_posiciones
lista_posiciones = matriz_descendencia
return lista_posiciones, fitness_mejor_individuo
Ejecutamos el algoritmo genético al completo
datos_ordenados = cargar_datos()
# Generamos la población inicial
lista_posiciones = generar_poblacion_inicial(datos_ordenados, num_act_min = 2, num_act_max = 20)
fitness_mejor_individuo = 0
generaciones_sin_mejora = 0
generacion = 0
while generaciones_sin_mejora < 100:
generacion += 1
# Calculamos la función de fitness a la generación actual
lista_fitness = list()
lista_pesos_carteras_fitness = list()
for cartera in range(len(lista_posiciones)):
fitness, pesos_fitness = calcular_fitness(datos_ordenados = datos_ordenados, posiciones = lista_posiciones[cartera])
lista_fitness.append(fitness)
lista_pesos_carteras_fitness.append(pesos_fitness)
# Guardamos el mejor individuo de la generación actual
if fitness_mejor_individuo < max(lista_fitness):
fitness_mejor_individuo = max(lista_fitness)
posicion_mejor_individuo = np.where(lista_fitness == fitness_mejor_individuo)
pesos_cartera_mejor_individuo = lista_pesos_carteras_fitness[posicion_mejor_individuo[0][0]]
activos_cartera_mejor_individuo = lista_posiciones[posicion_mejor_individuo[0][0]]
print(f'Generación {generacion}. El mejor individuo tiene una eficiencia de {fitness_mejor_individuo}')
generaciones_sin_mejora = 0
else:
print(f'Generación {generacion+1}. Sin mejora generacional respecto a la anterior')
generaciones_sin_mejora += 1
# Llevamos a cabo la selección de padres, cruzamiento, mutación y matriz de descendencia
lista_posiciones, fitness_mejor_individuo = reemplazo_generacional(datos_ordenados, lista_posiciones, lista_fitness, lista_pesos_carteras_fitness, activos_cartera_mejor_individuo)
print(fitness_mejor_individuo)
print(activos_cartera_mejor_individuo)
print(pesos_cartera_mejor_individuo)
- ¿Qué diferencia hay con el método anterior?
- De necesitar 24 horas a emplear solo un minuto y medio
- De una cartera con una eficiencia de 0.6226 a una de 1.5073
- De necesitar un I9 con 64 GB de RAM a usar cualquier portátil doméstico
Y este es solo un ejemplo del aporte que realiza la Inteligencia Artificial a las finanzas
