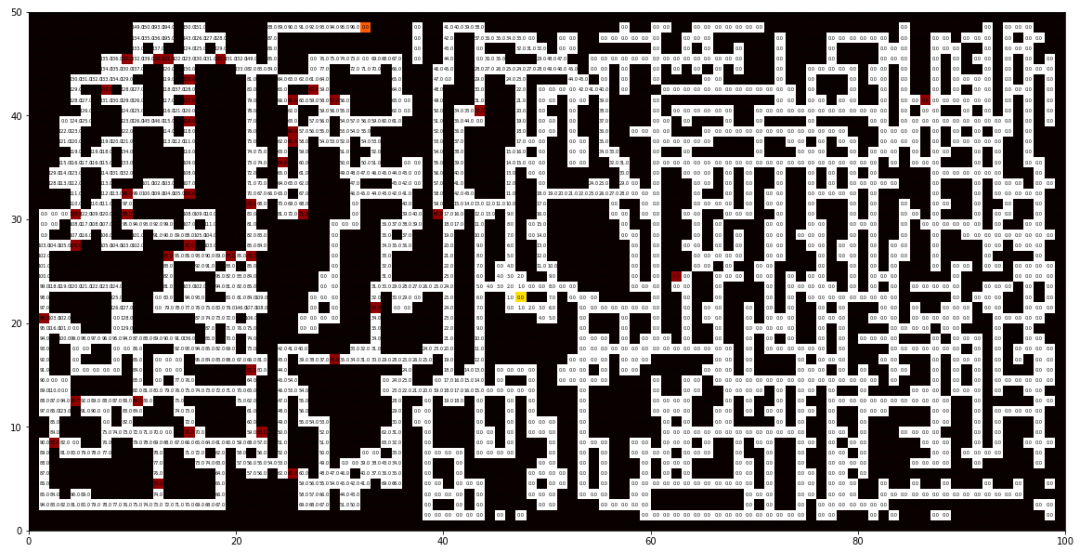
Reto de la exploración optimizada
Un sistema multiagente (SMA) es un sistema compuesto por múltiples agentes que interactúan entre ellos. Los agentes no tienen por qué ser necesariamente inteligentes, a nivel individual.
Un sistema multiagente es un sistema distribuido en el cual los elementos son sistemas de inteligencia artificial, o bien un sistema distribuido donde la conducta combinada de dichos elementos produce un resultado en conjunto inteligente.
Es decir, hay dos enfoques para construir sistemas multiagentes:
El enfoque formal o clásico, que consiste en dotar de los agentes de la mayor inteligencia posible utilizando descripciones formales del problema que resolver.
El enfoque constructivista, que persigue la idea de brindarle inteligencia al conjunto de todos los agentes, para que, a través de mecanismos de interacción, el sistema mismo genere comportamiento inteligente que no necesariamente estaba definido dentro de los agentes mismos (que pueden ser realmente simples). Este tipo de conducta es habitualmente llamado comportamiento emergente.
Ventajas: Solucionan problemas complejos en un periodo de tiempo aceptable, siendo un sistema muy robusto a mínimos locales. Al ser los agentes, elementos independientes, es muy sencillo paralelizar su comportamiento.
Desventajas: No garantizan una solución óptima.
Existen multitud de sistemas multi-agente
- Optimización de la colonia de hormigas: algoritmos de optimización inspirada en las acciones de una colonia de hormigas. Método muy útil en problemas que necesitan encontrar caminos hacia metas. El objetivo es localizar soluciones óptimas moviéndose a través de un espacio de parámetros que representa todas las posibles soluciones. Las hormigas naturales utilizan las feromonas para orientarse entre ellas, señalizando los recursos y explorando su entorno.
- Algoritmo de manada
- Algoritmo de construcción de las termitas
En los últimos años han surgido multitud de algoritmos enjambre
- Optimización enjambre de partículas
- Optimización de múltiples enjambres
- Colonia de abejas
- Sistemas inmunológicos artificiales
- Búsqueda de sistema cargado
- Búsqueda gravitacional
- Caída inteligente de gotas de agua
- Optimización magnética
Si bien, este reto, se va a centrar en la optimización de la colonia de hormigas
Elementos de un sistema multiagente
- Entorno
- Es el problema que queremos resolver.
- Este es uno de los puntos más importantes del proceso, y por norma general no se le da la importancia necesaria. Cuando se estudian este tipo de algoritmos, se suele dar el entorno hecho para que el alumno se centre en el algoritmo. Pero sin diseñar el entorno, es imposible que se comprenda bien el algoritmo. Volveremos a esto en breve.
- Puede evolucionar con el paso del tiempo, ser modificable (o no), tener objetos (o no).
- Objetos
- Fuentes de alimento, bloques de construcción, ciudades que visitar, obstáculos que salvar… puede ser transportables (o no), temporales o permanentes. Las “BadZones” deben tener las características de alcance (radio) y tiempo restante de vida.
- Agentes
- Hay que definir el comportamiento de los agentes, las relaciones que tendrán entre sí (jerárquica o igual) y la comunicación entre ellos. Cada agente poseerá un conjunto de operaciones sobre los objetos (transportarlos, usarlos, señalarlos) y sobre los demás agentes (intercambiar objetos, información).
- Percepción del mundo
- Pueden tener una percepción global del entorno (ver el tablero completo, mapa completo, laberinto desde arriba) o una percepción localizada a su alrededor (como cuando estás dentro de un laberinto, solo puedes ver lo que tienes inmediatamente a tu alrededor). Distintos agentes podrían tener percepciones distintas del entorno.
- Toma de decisiones
- Debemos determinar cómo reaccionará un individuo en función de sus percepciones y unas reglas a aplicar (sistema experto, lógica difusa, redes neuronales). Con unas pocas reglas simples es posible resolver problemas muy complejos (las redes neuronales se basan en regresiones lineales). Se pueden agregar aspectos estocásticos (aleatoriedad) para permitir que el sistema sea más fluido y flexible.
- Cooperación y comunicación
- Debemos determinar cómo van a comunicarse los individuos. Podría ser con comunicación directa (dos individuos que se encuentran y utilizan un lenguaje) o comunicación asíncrona (dejando trazas en el entorno como las hormigas).
- Capacidad del agente
- Pueden tener todos las mismas capacidades o estar organizados en castas (donde cada uno tiene una tarea / capacidad distinta). Es posible que los agentes aprendan con el paso del tiempo o que tengan conocimientos fijos. Si se agrega aprendizaje hay que determinar al algoritmo de aprendizaje subyacente (redes neuronales, algoritmo genético…).
¿Qué usos podría tener un sistema multi agente?
Simulación de multitudes, análisis de reacciones en caso de evacuación, descubrir zonas de posibles aglomeraciones, planificación de tráfico, simulación de tropas, optimización de flotas de vehículos, organización de fábricas (búsqueda de rutas adaptándose a la circulación).
Pero también comprensión de fenómenos complejos, como el crecimiento de poblaciones de bacterias, control de vehículos no tripulados, la Nasa lo está estudiando para el autoensamblaje orbital, cartografía planetaria, detección y eliminación de tumores dentro del cuerpo, a través de nanorobots.
O para la minería. Ya sea de datos, o minería real.
Como veis, tiene multitud de aplicaciones.
¿Cuándo deberíamos usarlos?
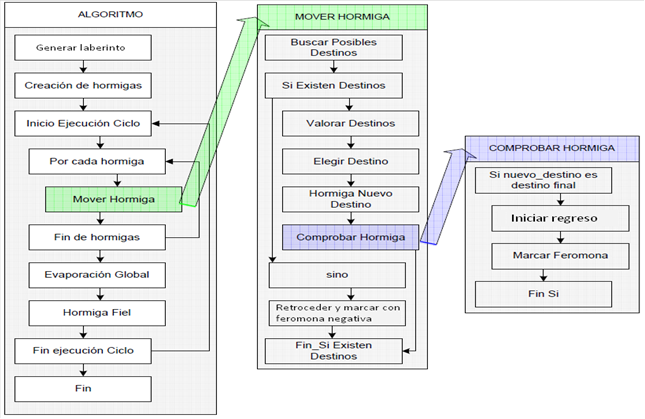
Funcionamiento del algoritmo ACO
Las hormigas se comunican mediante feromonas depositadas en el suelo. Las exploradoras se desplazan aleatoriamente por el entorno, cuando encuentran comida, vuelven al hormiguero por el mismo camino dejando un rastro de feromonas (las hormigas recuerdan perfectamente cada paso que han realizado).
Las demás exploradoras que encuentran la feromona tienen tendencia a seguirla (la probabilidad depende de la cantidad de feromona depositada).
Las feromonas se evaporan de manera natural.
Siguiendo este sistema, las hormigas son capaces de determinar el camino más corto entre la colonia y el alimento.
Generación del entorno
Necesitamos un generador de entornos a resolver
En este caso, un generador de laberintos, que sea capaz de generar entornos con 0, 1 o N soluciones. Para que podamos poner a prueba el algoritmo, y ver qué tal funciona.
La generación de entornos es uno de los puntos más importantes a la hora de extrapolar conocimientos y adquirir la capacidad de resolver problemas con inteligencia artificial.
Prestar atención a la construcción de tu propio entorno es esencial (en vez de que te den uno hecho). Por ejemplo:
¿Son estos dos laberintos semejantes?

No
Aunque ambos tienen N soluciones, el de la izquierda tiene un problema de “rotondas” y el de la derecha de “rotondas +”plazas”. Por lo que es más complejo de resolver para las hormigas.
Reto de la exploración optimizada
En las páginas siguientes os facilito el código que genera, y resuelve un laberinto con rotondas y plazas (como el de la derecha). Sin embargo, la exploración es “ineficiente” debido a la existencia de ambos elementos.
¿Eres capaz de encontrar y programar una solución a ambos problemas, sin tocar la generación del laberinto?
Manda tu solución a gmelendez@grupobme.es
Guillermo Meléndez Alonso
Responsable del laboratorio de Inteligencia Artificial en Bolsas y Mercados Españoles Inntech
Director del máster de Inteligencia Artificial Aplicada a los Mercados Financieros en Instituto BME
Código para resolver laberinto con rotondas
import pandas as pd
import numpy as np
import random
import matplotlib.pyplot as plt
from IPython.display import clear_output
import time
import PySimpleGUI as sg
import easygui
class ant:
def __init__(self ,laberinto, hormiguero, muro, pasillo, comida, hormiga):
self.muro = muro
self.pasillo = pasillo
self.hormiguero = hormiguero
self.comida = comida
self.hormiga = hormiga
self.lista_movimientos = list()
self.lista_movimientos.append(np.array(np.where(laberinto == hormiguero))[:,0])
self.comida_encontrada = False
def moverse(self, laberinto, matriz_feromonas, matriz_fiel):
self.comida_encontrada = False
# Debemos anular la opción de que retroceda por donde ha venido.
mov_posibles = np.copy(matriz_feromonas)
if len(self.lista_movimientos) > 1:
mov_posibles[self.lista_movimientos[-2][0],self.lista_movimientos[-2][1]] = 0
# La hormiga mira alrededor para determinar cuantas opciones de camino tiene
subir = mov_posibles[self.lista_movimientos[-1][0]-1, self.lista_movimientos[-1][1]]
bajar = mov_posibles[self.lista_movimientos[-1][0]+1, self.lista_movimientos[-1][1]]
izq = mov_posibles[self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]-1]
der = mov_posibles[self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]+1]
# Debemos comprobar cuantas opciones de movimiento tiene. Si no tiene ninguna, debe retroceder y "anular" la casilla.
if subir + bajar + izq + der == 0:
if laberinto[self.lista_movimientos[-1][0],self.lista_movimientos[-1][1]] != self.hormiguero:
# Retrocedemos una posición y anulamos la casilla, para que ninguna otra hormiga la pise
matriz_feromonas[self.lista_movimientos[-1][0],self.lista_movimientos[-1][1]] = 0
laberinto[self.lista_movimientos[-1][0],self.lista_movimientos[-1][1]] = self.muro
del self.lista_movimientos[-1]
else:
# Si no la reiniciamos, se queda bloqueada en el hormiguero.
self.matar_hormiga(laberinto)
else:
# Decidimos movimiento "aleatoriamente" en función de las feromonas
# Comparamos el número aleatorio con la distribución actual de feromonas por cada casilla.
# El intervalo en el que esté el número aleatorio será la dirección que elegirá.
# Ej con tres posibles caminos a=20% , b=50%, c=30%, si el número aleatorio sale 75% --> 75>20 (no lo elije), 75>20+50 (no lo elije), 75<(20+50+30) (lo elije)
feromona_total = subir + bajar + izq + der
subir = subir / feromona_total
bajar = bajar / feromona_total
izq = izq / feromona_total
der = der / feromona_total
posibilidades = np.array([subir, bajar, izq, der])
prox_mov = np.random.rand()
for pos in range(len(posibilidades)):
if prox_mov < sum(posibilidades[0:pos+1]):
break
if pos == 0: # Subimos
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0]-1, self.lista_movimientos[-1][1]]))
elif pos == 1: # Bajamos
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0]+1, self.lista_movimientos[-1][1]]))
elif pos == 2: # Izquierda
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]-1]))
else: # Derecha
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]+1]))
# Comprobamos la distancia que ha recorrido la hormiga. Si está perdida, la "matamos de hambre"
if len(self.lista_movimientos) > (laberinto.shape[0] * laberinto.shape[1]):
self.matar_hormiga(laberinto)
else:
# Mostramos el movimiento
self.mostrar_movimiento(laberinto)
# Si hemos encontrado la comida, depositamos las feromonas
if laberinto[self.lista_movimientos[-1][0],self.lista_movimientos[-1][1]] == self.comida:
self.depositar_feromonas(laberinto, matriz_feromonas, matriz_fiel)
def mostrar_movimiento(self, laberinto):
# Mostramos el movimiento visualmente (debemos comprobar que no es el hormiguero ni la comida)
if laberinto[self.lista_movimientos[-1][0],self.lista_movimientos[-1][1]] == self.pasillo:
laberinto[self.lista_movimientos[-1][0],self.lista_movimientos[-1][1]] = self.hormiga
# Borramos el movimiento anterior (volviendo a ser un pasillo)
if len(self.lista_movimientos) > 1:
if laberinto[self.lista_movimientos[-2][0],self.lista_movimientos[-2][1]] == self.hormiga:
laberinto[self.lista_movimientos[-2][0],self.lista_movimientos[-2][1]] = self.pasillo
def matar_hormiga(self, laberinto):
# Borramos visualmente la hormiga muerta
if laberinto[self.lista_movimientos[-2][0],self.lista_movimientos[-2][1]] == self.hormiga:
laberinto[self.lista_movimientos[-2][0],self.lista_movimientos[-2][1]] = self.pasillo
self.lista_movimientos = list()
self.lista_movimientos.append(np.array(np.where(laberinto == self.hormiguero))[:,0])
def depositar_feromonas(self, laberinto, matriz_feromonas, matriz_fiel):
# Podamos la solución encontrada y depositamos las feromonas
self.poda_solucion(laberinto, matriz_feromonas, matriz_fiel)
# Matamos la hormiga
self.comida_encontrada = True
self.matar_hormiga(laberinto)
def poda_solucion(self, laberinto, matriz_feromonas, matriz_fiel):
lista_movimientos = [list(x) for x in self.lista_movimientos]
# Posiciones sin repetición a chequear (para iterar sobre ellas)
pos_unicas = map(tuple, lista_movimientos)
pos_unicas = set(pos_unicas)
lista_pos_uni = [list(x) for x in pos_unicas]
# Localizamos y borramos todos los bucles que haya realizado la hormiga
distancia_maxima = 1
while distancia_maxima > 0:
# Calcular la distancia entre repeticiones, buscando el mayor bucle a eliminar
distancia_maxima = 0
for val in lista_pos_uni:
# Localización de repeticiones (cuando ha vuelto a estar en la misma celda)
repeticiones = [i for i, j in enumerate(lista_movimientos) if j == val]
if len(repeticiones) > 0:
distancia = repeticiones[-1] - repeticiones[0]
if distancia > distancia_maxima:
distancia_maxima = distancia
# Eliminamos el bucle identificado
inicio = repeticiones[0]
fin = repeticiones[-1]
lista_movimientos[inicio:fin] = []
# Mostramos el camino y depositamos las feromonas, excepto la 1ª y última posición (hormiguero, comida)
for paso in range(1, len(lista_movimientos)-1):
laberinto[lista_movimientos[paso][0],lista_movimientos[paso][1]] = 6
matriz_feromonas[lista_movimientos[paso][0],lista_movimientos[paso][1]] += 1/len(self.lista_movimientos)
# Evaporamos un porcentaje de las feromonas de las casillas
matriz_feromonas[laberinto==self.pasillo] = matriz_feromonas[laberinto==self.pasillo] * 0.9
# Reconstruimos el camino que ha seguido, para la hormiga fiel
for paso in range(1, len(lista_movimientos)-1):
if matriz_fiel[lista_movimientos[paso][0], lista_movimientos[paso][1]] > (len(lista_movimientos) - paso -1):
matriz_fiel[lista_movimientos[paso][0], lista_movimientos[paso][1]] = (len(lista_movimientos) - paso -1)
# Pintamos el laberinto con la ruta seguida y la asignación de feromonas.
self.pinta_laberinto(laberinto, matriz= matriz_feromonas, mostrar = False)
time.sleep(1)
# Borramos el camino, para que el programa pueda continuar
laberinto[laberinto==6] = self.pasillo
def movimiento_fiel(self, laberinto, matriz_fiel):
# Miramos alrededor
subir = matriz_fiel[self.lista_movimientos[-1][0]-1, self.lista_movimientos[-1][1]]
bajar = matriz_fiel[self.lista_movimientos[-1][0]+1, self.lista_movimientos[-1][1]]
izq = matriz_fiel[self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]-1]
der = matriz_fiel[self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]+1]
if subir == min(subir, bajar, izq, der):
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0]-1, self.lista_movimientos[-1][1]]))
elif bajar == min(subir, bajar, izq, der):
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0]+1, self.lista_movimientos[-1][1]]))
elif izq == min(subir, bajar, izq, der):
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]-1]))
else:
self.lista_movimientos.append(np.array([self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]+1]))
# Marcamos el movimiento en el laberinto
laberinto[self.lista_movimientos[-1][0], self.lista_movimientos[-1][1]] = 8
def pinta_laberinto(self, laberinto, matriz, mostrar = False):
if mostrar == False:
clear_output(wait=True)
plt.figure(figsize = (laberinto.shape[0]/2.5, laberinto.shape[1]/2.5))
plt.imshow(laberinto, cmap='hot')
plt.show()
else:
# Mostramos la cantidad de feromonas que tiene cada celda
clear_output(wait=True)
values = matriz
# Limites para cuadrar el texto
x_start = 0
x_end = laberinto.shape[1]
y_start = 0
y_end = laberinto.shape[0]
extent = [x_start, x_end, y_start, y_end]
# Creamos el gráfico normal
fig = plt.figure(figsize = (laberinto.shape[0]/2.5, laberinto.shape[1]/2.5))
ax = fig.add_subplot(111)
im = ax.imshow(laberinto, extent=extent, cmap='hot')
# Añadimos el texto
jump_x = (x_end - x_start) / (2.0 * laberinto.shape[1])
jump_y = (y_end - y_start) / (2.0 * laberinto.shape[0])
x_positions = np.linspace(start=x_start, stop=x_end, num=laberinto.shape[1], endpoint=False)
y_positions = np.linspace(start=y_start, stop=y_end, num=laberinto.shape[0], endpoint=False)
if laberinto.shape[0] < 70 and laberinto.shape[1] < 70 and laberinto.shape[0] == laberinto.shape[1]:
tamaño_letra = 8
else:
tamaño_letra = 5
for y_index, y in enumerate(reversed(y_positions)):
for x_index, x in enumerate(x_positions):
label = values[y_index, x_index]
text_x = x + jump_x
text_y = y + jump_y
ax.text(text_x, text_y, label, color='black', ha='center', va='center', size=tamaño_letra)
plt.show()
class laberinto:
def __init__(self):
self.muro = 0
self.pasillo = 10
self.hormiguero = 5
self.comida = 7
self.hormiga = 2
def aco(self):
try:
# Construimos el laberinto y depositamos las feromonas iniciales
self.laberinto, self.matriz_feromonas, self.matriz_fiel = self.construye_laberinto(muro = self.muro, pasillo = self.pasillo, hormiguero = self.hormiguero, comida = self.comida)
# El número de hormigas dependerá del tamaño del laberinto
n_hormigas = int(round((sum(self.laberinto.shape)/2)))
lista_hormigas = [ant(self.laberinto, muro = self.muro, pasillo = self.pasillo, hormiguero = self.hormiguero,
comida = self.comida, hormiga = self.hormiga) for ele in range(n_hormigas)]
# Comprobamos movimientos
veces_comida_encontrada = 0
iteraciones = 0
while veces_comida_encontrada < (self.laberinto.shape[0]*self.laberinto.shape[1]/100):
iteraciones += 1
if iteraciones > self.laberinto.shape[0]*self.laberinto.shape[1] and veces_comida_encontrada == 0:
easygui.msgbox("Este laberinto no tiene solución.\n \nCuando el laberinto es muy pequeño esto puede pasar.\n \nVuelve a intentarlo con uno más grande.\n \n",
title="Conclusión")
break
for ele in lista_hormigas:
ele.moverse(laberinto= self.laberinto, matriz_feromonas= self.matriz_feromonas, matriz_fiel= self.matriz_fiel)
if ele.comida_encontrada == True:
veces_comida_encontrada += 1
self.pinta_laberinto(self.laberinto, matriz= self.matriz_feromonas, mostrar = False)
# Hormiga fiel
if veces_comida_encontrada > 0:
fiel = ant(self.laberinto, muro = self.muro, pasillo = self.pasillo, hormiguero = self.hormiguero,
comida = self.comida, hormiga = self.hormiga)
while self.matriz_fiel[fiel.lista_movimientos[-1][0], fiel.lista_movimientos[-1][1]] != 1:
fiel.movimiento_fiel(self.laberinto, self.matriz_fiel)
self.pinta_laberinto(self.laberinto, matriz= self.matriz_feromonas, mostrar = False)
self.laberinto[self.laberinto==8] = self.pasillo
easygui.msgbox("Solución encontrada", title="Camino óptimo")
except:
print("""Los laberintos pueden tener 0, 1, o N soluciones. Aunque pasa muy pocas veces, es posible que el hormiguero esté atrapado
y las hormigas no tengan adonde ir. No pasa nada, símplemente, inténtalo de nuevo""")
def pinta_laberinto(self, laberinto, matriz, mostrar = False):
if mostrar == False:
clear_output(wait=True)
plt.figure(figsize = (laberinto.shape[0]/2.5, laberinto.shape[1]/2.5))
plt.imshow(laberinto, cmap='hot')
plt.show()
else:
# Mostramos la cantidad de feromonas que tiene cada celda
clear_output(wait=True)
values = matriz
# Limites para cuadrar el texto
x_start = 0
x_end = laberinto.shape[1]
y_start = 0
y_end = laberinto.shape[0]
extent = [x_start, x_end, y_start, y_end]
# Creamos el gráfico normal
fig = plt.figure(figsize = (laberinto.shape[0]/2.5, laberinto.shape[1]/2.5))
ax = fig.add_subplot(111)
im = ax.imshow(laberinto, extent=extent, cmap='hot')
# Añadimos el texto
jump_x = (x_end - x_start) / (2.0 * laberinto.shape[1])
jump_y = (y_end - y_start) / (2.0 * laberinto.shape[0])
x_positions = np.linspace(start=x_start, stop=x_end, num=laberinto.shape[1], endpoint=False)
y_positions = np.linspace(start=y_start, stop=y_end, num=laberinto.shape[0], endpoint=False)
if laberinto.shape[0] < 70 and laberinto.shape[1] < 70 and laberinto.shape[0] == laberinto.shape[1]:
tamaño_letra = 8
else:
tamaño_letra = 5
for y_index, y in enumerate(reversed(y_positions)):
for x_index, x in enumerate(x_positions):
label = values[y_index, x_index]
text_x = x + jump_x
text_y = y + jump_y
ax.text(text_x, text_y, label, color='black', ha='center', va='center', size=tamaño_letra)
plt.show()
def tamaño_laberinto(self):
layout = [[sg.Text("¿Cómo quieres de alto el laberinto? \n \nPrueba con 50, por ejemplo")],
[sg.Input()],
[sg.Button('Ok')] ]
sg.theme('Reddit')
window = sg.Window('Selección de alto ', layout, finalize = True)
window.BringToFront()
event, alto = window.read()
window.close()
layout = [[sg.Text("¿Cómo quieres de ancho el laberinto? \n \nPrueba con 100, por ejemplo")],
[sg.Input()],
[sg.Button('Ok')] ]
sg.theme('Reddit')
window = sg.Window('Selección de ancho ', layout, finalize = True)
window.BringToFront()
event, ancho = window.read()
window.close()
try:
alto = int(alto[0])
ancho = int(ancho[0])
except:
print("Debes indicar un número para el tamaño")
alto, ancho = tamaño_laberinto()
return alto, ancho
def construye_laberinto(self, muro = 0, pasillo = 10, hormiguero = 5, comida = 7):
'''
Lo primero que debemos hacer es construir un entorno en el que podamos poder a prueba la colonia de hormigas
Este punto es muy importante. La manera en la que construyamos el laberinto puede hacer que sea muy fácil de resolver (solo haya una solución)
Queremos generar laberintos aleatorios que puedan tener entre 0 y N soluciones
Por otro lado, el cómo hagamos los caminos puede derivar en "rotondas" (como en la solución de excel), o "plazas" (como está programado aquí)
En estas rotondas o plazas será donde la hormiga tendrá más dificultad a la hora de orientarse
Por otro lado, La relación entre la feromona inicial y la feromono depositada (en función a la distancia) debe estar en perfecto equilibrio o el enjambre no funcionará
Prestad atención a que la cantidad de feromona inicial es muy distinta si el laberinto es cuadrado u horizontal. Hay que prestar mucha atención a este punto
'''
alto, ancho = self.tamaño_laberinto()
laberinto = np.zeros((alto, ancho))
# Construimos los caminos del laberinto
for camino in range(int(round((alto * ancho)/ 5))):
inicio_ok = False
while inicio_ok == False:
fila = np.random.randint(low = 1, high = alto-1, size = 1)
columna = np.random.randint(low = 1, high = ancho -1, size = 1)
if laberinto[fila, columna] == muro:
inicio_ok = True
if camino == 0:
laberinto[fila, columna] = hormiguero
else:
laberinto[fila, columna] = pasillo
# A partir de la posición inicial, comenzamos a "tirar muros"
# Condiciones de parada: que llegue a un pasillo o al muro exterior
direccion = np.random.randint(low = 1, high = 4, size = 1)
stop = False
pos_fila = fila
pos_col = columna
longitud = 0
while stop == False:
if direccion == 1: # subimos
# Comprobamos que la nueva posición es un muro y que no está en los límites
if (laberinto[pos_fila - 1, pos_col] == muro and (pos_fila - 1) != 0 and laberinto[pos_fila, pos_col +1] == muro and laberinto[pos_fila, pos_col -1] == muro and longitud < round(laberinto.shape[0]/4)):
laberinto[pos_fila - 1, pos_col] = pasillo
pos_fila = pos_fila - 1
longitud += 1
else:
stop = True
elif direccion == 2: # bajamos
# Comprobamos que la nueva posición es un muro y que no está en los límites
if (laberinto[pos_fila + 1, pos_col] == muro and (pos_fila + 1) != laberinto.shape[0]-1 and laberinto[pos_fila, pos_col +1] == muro and laberinto[pos_fila, pos_col -1] == muro and longitud < round(laberinto.shape[0]/4)):
laberinto[pos_fila + 1, pos_col] = pasillo
pos_fila = pos_fila + 1
longitud += 1
else:
stop = True
elif direccion == 3: # vamos a la derecha
# Comprobamos que la nueva posición es un muro y que no está en los límites
if (laberinto[pos_fila, pos_col + 1] == muro and (pos_col + 1) != laberinto.shape[1]-1 and laberinto[pos_fila +1, pos_col] == muro and laberinto[pos_fila-1, pos_col] == muro and longitud < round(laberinto.shape[0]/4)):
laberinto[pos_fila, pos_col + 1] = pasillo
pos_col = pos_col + 1
longitud += 1
else:
stop = True
else: # vamos a la izquierda
# Comprobamos que la nueva posición es un muro y que no está en los límites
if (laberinto[pos_fila, pos_col - 1] == muro and (pos_col - 1) != 0 and laberinto[pos_fila +1, pos_col] == muro and laberinto[pos_fila-1, pos_col] == muro and longitud < round(laberinto.shape[0]/4)):
laberinto[pos_fila, pos_col - 1] = pasillo
pos_col = pos_col - 1
longitud += 1
else:
stop = True
# La última posición será la comida
laberinto[fila, columna] = self.comida
# La relación entre la feromona inicial y la feromono depositada (en función a la distancia) debe estar en perfecto equilibrio o el enjambre no funcionará
feromona_inicial = 1 / (sum(laberinto.shape)/2)
# Depositamos la feromona inicial en todas las casillas que no sean muros
matriz_feromonas = np.zeros((laberinto.shape[0], laberinto.shape[1]))
matriz_feromonas[laberinto != muro] = feromona_inicial
# Depositamos una feromona muy alta en la comida, para que si pasan a su lado, la vean.
matriz_feromonas[laberinto == comida] = feromona_inicial*1000
# Por último, pintamos el laberinto terminado
self.pinta_laberinto(laberinto, matriz= matriz_feromonas, mostrar = False)
# Creamos una matriz_fiel para la hormiga fiel
matriz_fiel = np.copy(laberinto)
matriz_fiel[laberinto == self.muro] = 1000
matriz_fiel[laberinto == self.pasillo] = 1000
matriz_fiel[laberinto == self.hormiguero] = 1000
matriz_fiel[laberinto == self.comida] = 0
return laberinto, matriz_feromonas, matriz_fiel
def mostrar_matriz_feromonas(self):
# Mostramos la matriz de feromonas
self.matriz_feromonas = np.round(self.matriz_feromonas, 2)
self.pinta_laberinto(self.laberinto, matriz = self.matriz_feromonas, mostrar = True)
def mostrar_matriz_hormiga_fiel(self):
# Mostramos las rutas para la hormiga fiel
self.matriz_fiel[self.matriz_fiel==1000]=0
self.matriz_fiel = np.round(self.matriz_fiel, 0)
self.pinta_laberinto(self.laberinto, matriz = self.matriz_fiel, mostrar = True)
Instanciamos el laberinto a resolver por el método Ant Colony Optimization
laberinto_a_resolver = laberinto()
laberinto_a_resolver.aco()

También podemos mostrar la matriz de feromonas que guía a las hormigas
El laberinto puede ser tan complejo como nosotros queramos
matriz de feromonas que guía a las hormigas
laberinto_a_resolver.mostrar_matriz_feromonas()
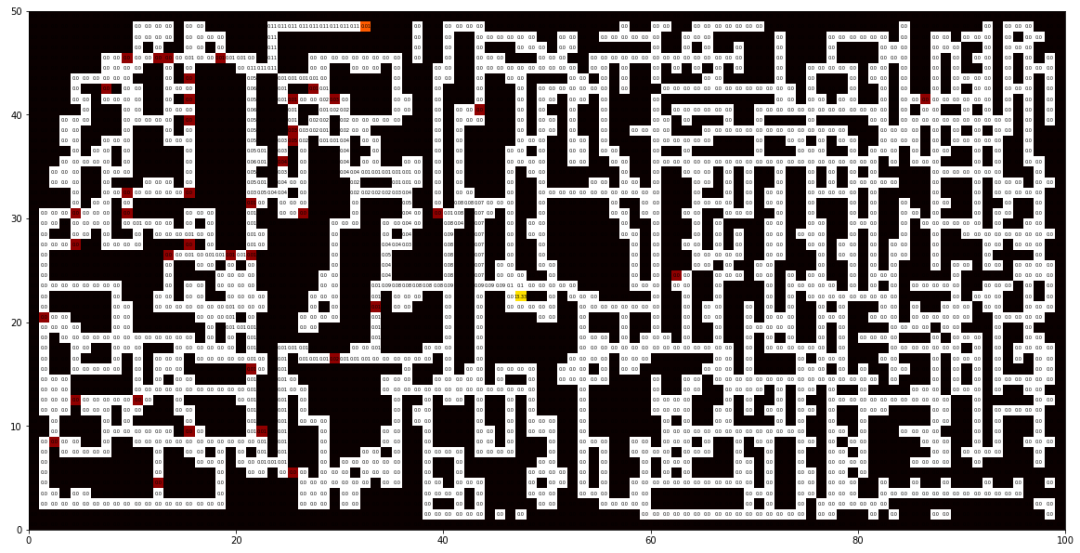
Así como mostrar la matriz de caminos de la hormiga fiel
Matriz de caminos de la hormiga fiel
laberinto_a_resolver.mostrar_matriz_feromonas()